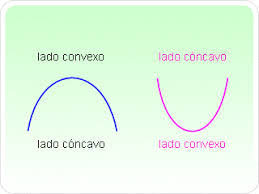
Función convexa o cóncava hacia abajo

Podemos determinar las funciones convexa y concaba hacia arriba utilizando el criterio de la segunda derivada y algunos ejemplos. 

Ejercicios de ejemplo

Ejercicio 1: Función Cuadrática

Consideremos la función:F(incógnita)=−incógnita2f ( x )=- x2

• Primera Derivada :

F"(incógnita)=−2incógnitaF"( x )=- 2x​

• Segunda Derivada :

F""(incógnita)=−2F"( x )=− 2Dado queF""(incógnita)=−2<0F"( x )=− 2<0para todoincógnitaincógnita, la funciónF(incógnita)=−incógnita2f ( x )=- x2es cóncava hacia abajo en todoRR.

Ejercicio 2: Función Cúbica

Consideremos la función:gramo(incógnita)=−incógnita3+3incógnita2g ( x )=- x3+3 veces2

• Primera Derivada :

gramo"(incógnita)=−3incógnita2+6incógnitagramo"( x )=- 3 x2+6x​

• Segunda Derivada :

gramo""(incógnita)=−6incógnita+6gramo"( x )=- 6x​+6Para encontrar los intervalos de concavidad, resolvemosgramo""(incógnita)≤0gramo"( x )≤0:−6incógnita+6≤0  ⟹  incógnita≥1- 6x​+6≤0⟹incógnita≥1Por lo tanto,gramo(incógnita)g ( x )es cóncava hacia abajo en el intervalo[1,∞)[ 1 ,∞ ).

Ejercicio 3: Función Exponencial Negativa

Consideremos la función:yo(incógnita)=−miincógnitah ( x )=- miincógnita

• Primera Derivada :

yo"(incógnita)=−miincógnitayo"( x )=- miincógnita

• Segunda Derivada :

yo""(incógnita)=−miincógnitayo"( x )=- miincógnitaDado queyo""(incógnita)=−miincógnita<0yo"( x )=- miincógnita<0para todoincógnitaincógnita, la funciónyo(incógnita)=−miincógnitah ( x )=- miincógnitaes cóncava hacia abajo en todoRR.

Ejercicio 4: Función Logarítmica Negativa

Consideremos la función:a(incógnita)=−En⁡(incógnita)k ( x )=−en ( x )En el intervalo(0,∞)( 0 ,∞ ).

• Primera Derivada :

a"(incógnita)=−1incógnitaa"( x )=−incógnita1​

• Segunda Derivada :

a""(incógnita)=1incógnita2a"( x )=incógnita21​Dado quea""(incógnita)>0a"( x )>0, esta función no es cóncava hacia abajo. Sin embargo, si consideramos la función negativa de esta, comometro(incógnita)=−a(incógnita)=En⁡(incógnita)m ( x )=− k ( x )=en ( x ), podemos ver que esta es convexa hacia arriba.